LLM（大規模言語モデル）の仕組みを追っている中で、シグモイド関数やソフトマックス関数を咀嚼する必要が出てきて、それらの中で使われている自然対数（eの何乗というやつです）が自然対数である必然性があるのか気になってしまい、ネイピア数（そのeのこと）についておさらいと考察をしましたので、そのことを書きます。

■ネイピア数の定義

まずネイピア数（e）の定義は以下で、計算すると2.718・・・の無理数（分数では表せない数字）になります。
（定義の１つだと言われている向きもありますが、定義が複数あるってことありえるのかは疑問に思っています。）

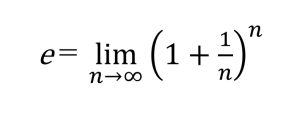
■ネイピア数がらみの代表的な定理

ネイピア数を使ったら下記のようになったというより、下記のような性質を持つ値を探し出して（作り出して）ネイピア数としていると理解しています。

１）ネイピア数（e）を底とするeのx乗という指数関数を微分した場合に同じ式eのx乗になる。

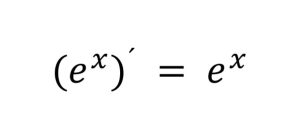
２）ネイピア数（e）を底としxを真数とした対数関数を微分した場合、x分の1になる。

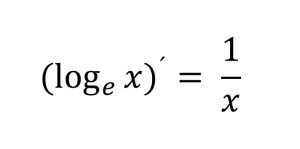
ネイピア数（e）って何だったっけ？のメモは以上なので、ざっくり思い出したい場合はここで終了です。

ーーーーーーーーーーーーーーーーーーーーーーーーーーー

ここからは私のつぶやき強め、出口のないラビリンスですので、暇をもてあましている方以外は読み飛ばしてください。

はるか昔ではありますが、ネイピア数を少しは扱ってはおりましたので、以上の定義や定理は「ああ、そうだったな」と思い出す感じではありました。
ただ、「e」を戦闘員気分で「イー！」としか読んでいなかったので、ネイピア数という名前が付いていることは憶えていませんでした。

この度、なぜにわざわざネイピア数こと「e」について再確認したかというと、冒頭にも書いた通り、LLMやその前段のディープラーニングの仕組みを追っている中、パラーメータの重み付けをする活性化関数として利用されているシグモイド関数やソフトマックス関数に使われているネイピア数を見て、ネイピア数であることの必然性が気になってしまったからです。

つまり下記のようでなく

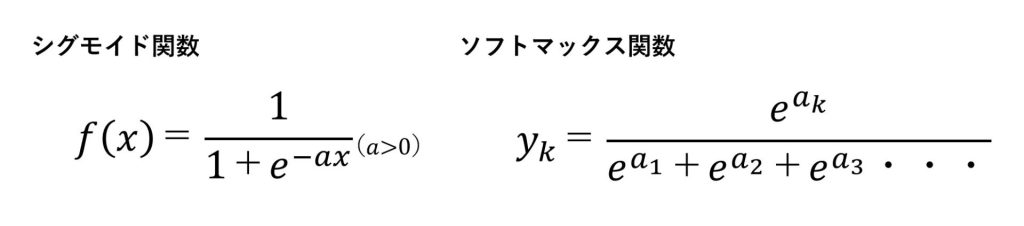
下記のようにeを適当な実数にしたものではだめなのかな？と思い
（自然数、特に2とかを使った方がマシンパワーにはやさしいのでは？）

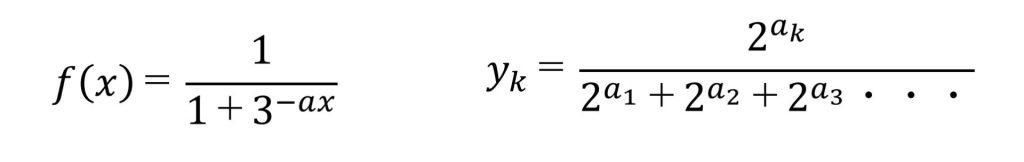
ネイピア数の定義や以上の定理を再確認しましたが、それでは必然性が見いだせず、それ以外の便利機能ってないのかな？とあくせくしているうちにネイピア数の起こりも調べることになってしまいました。（ネイピア数って高校くらいの数学で突如として登場してきましたよね）

16~17世紀ごろに、ネイピア数の近似値の最古の文献を書いた人の名前からネイピアという名前がついた模様。

ネイピア数の定義のlimitの中の下記式は、もともと福利の計算から起こったそう。
（このあたりまでは、私のような凡庸な人間でもギリ思い付きそう。）

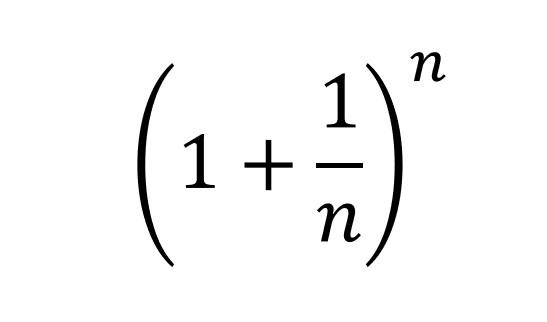
上記のnの値を無限大に近づけていったとき、算出される値の重要性を見出した方が18世紀ごろにいた模様。（諸説あり）
「微分がしたい」と片っ端から色々な数式を微分しつくしていって発見したのか？「微分しても同じ式になるものを算出してみよう」とある日思い立ったのか？その思いは計り知れず。

そして、極限に近づいた時のeの値2.718・・は小数点以下1000桁以上まで計算しているものもあるのですが、そんな計算を誰がいつ頃どうやったのか？下記のようなものを計算したのか？その労苦は計り知れず。

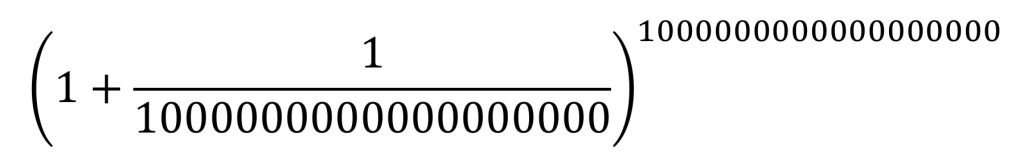
結果、やはり対数関数や微積分で利用する文脈以外での便利機能はなさそう。

ーーーーーーーーーーーーーーーーーーーーーーーーーーー

ディープラーニング入口のドアノブに手をかけて、静電気でパチッとしたくらいの段階ではありますが、あれやこれや調べた感じの一応の結論です。

・活性化関数として利用されるシグモイド関数やソフトマックス関数では、その性質の一部を利用したいという意味合いが強そうなので、おそらくネイピア数であることの必然性は低く、ネイピア数でない任意の実数（1より大きい正の数である必要はあり）を使ったとしても、係数などの重み付け調整などで正常に機能しそう。（Pythonのライブラリも使いたいので、あえて別の値を使う必要もないと思っていますが）

・ネイピア数は2.7くらいの実数であるということだけ憶えておけば、さしあたり問題なさそう。

・考え始めたらキリがないことになってしまったので、先人の知恵をありがたく拝借して便利に使わせていただく方針が良さそう。

この先、さらにディープにディープラーニングを理解していく中で、ネイピア数である必然性が発見出来たら、また追記させていただきます。